
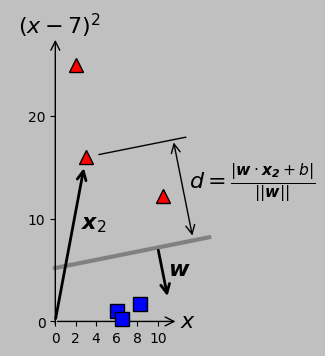
Here (look for ) you will find the cross, dot and || equations used if needed: This is equal to the perpendicular distance between the hyperplane and x, and is positive when x is on the same side of the plane as points and negative when x is on the opposite side. The last absolute value (on scalar distance) will just get rid of the sign of the result which tells you if the point p is in direction of normal n or in opposite one sometimes such info is wanted so in such case remove the outermost abs value and use polygon winding and cross product operands order to maintain wanted normal direction. Given a point x in n-dimensional space and a hyperplane described by and 0, find the signed distance between the hyperplane and x. We can exploit dot product for this so just crate a vector going from any point on the plane into your tested point and dot with unit normal. In this video Ill discuss about the very important topics- Find Perpendicular Distance from a Point to a Straight Line & Find Perpendicular Distance Betw. Of course, n x can also be expressed as n T x, and if we set n ( w 1, w 2, w 3) T, we have your boundary. This is calculated as the perpendicular distance from the line to support. Equation (1) tells us that the dot product of n with any point on the hyperplane is equal to the constant value d, so the distance of the hyperplane to the origin is n x n, where x is any point that satisfies (1). Point on plane closest to origin, for the. Particular instances include: Distance from a point to a line, for the perpendicular distance from a point to a line in two-dimensional space.

Let the triangle points be p0,p1,p2 and tested point p.įirst we need to obtain plane normal, that is simple vector multiplication of any two non parallel and non zero vectors inside the plane: n = cross( p1-p0, p2-p0 )Īnd normalize it to unit vector (to simplify stuff): n = n/|n| Support vectors are the data points, which are closest to the hyperplane. In geometry, the perpendicular distance between two objects is the distance from one to the other, measured along a line that is perpendicular to one or both. In principal one can use Lagrange multipliers and solve a large system of equations, but my attempt to do so met with a road block. I assume you want to compute perpendicular distance between point and plane given 3 points on it forming a triangle. distance from a point to a hyperplane There are many ways to solve this problem.


 0 kommentar(er)
0 kommentar(er)
